Say Goodbye to Blind Model Selection! ICML 2025 New Research Explains the Mysteries of Large Model Choice}

First author: Xinyue Zeng, PhD Candidate in Computer Science at Virginia Tech, focusing on interpretability and empirical performance of large language models. Corresponding author: Assistant Professor Dawei Zhou.

Struggling with efficient large language model (LLM) selection? Limited resources make exhaustive fine-tuning impossible? The latest research from Virginia Tech proposes the LensLLM framework, which accurately predicts fine-tuning performance and greatly reduces computational costs, making LLM selection no longer a “blind box.”

• Paper Title: LensLLM: Unveiling Fine-Tuning Dynamics for LLM Selection
• Authors: Xinyue Zeng, Haohui Wang, Junhong Lin, Jun Wu, Tyler Cody, Dawei Zhou
• Affiliations: Department of Computer Science, Virginia Tech, Blacksburg, VA, USA, etc.
• Open-source link: https://github.com/Susan571/LENSLLM
• Paper link: https://arxiv.org/abs/2505.03793

1. Introduction: Why is LLM selection a “bottleneck” amid rapid growth?

The wave of large language models (LLMs) is transforming NLP—from translation and summarization to chatbots. With open-source models like LLaMA, Falcon, Mistral, and DeepSeek emerging rapidly, finding the best model for specific tasks has become a major challenge. Traditional selection methods, which require massive computational resources and often lack generalization, are like groping in the dark, full of uncertainty.

2. Breakthrough in Theory: PAC-Bayesian Generalization Bound Reveals Deep Fine-Tuning Dynamics

To overcome this “bottleneck,” researchers at Virginia Tech proposed LensLLM, based on a novel PAC-Bayesian generalization bound. This framework reveals, for the first time, the “phase transition” dynamics of test loss (TestLoss) as a function of training data size (TrainSize) during fine-tuning.

Specifically, the PAC-Bayesian bound (Theorem 2) shows that the test loss of an LLM can be expressed as:

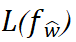
where n is the number of training samples, and it is closely related to the Hessian matrix of model parameters (which measures the curvature of the loss function and parameter sensitivity). Based on this, the team derived a simplified inference (Inference 1), which reduces the generalization bound to:

which indicates that the generalization performance depends on parameters related to the model and task. This theory uncovers the “dual-phase evolution” of fine-tuning performance:

• Pre-power phase: When data n is small, model behavior is dominated by initialization and early training dynamics, with high Hessian values and parameter sensitivity, leading to slow performance improvements.
• Power phase: As data n increases, the error scaling shifts to being dominated by task-related parameters, Hessian values decrease, and model stability improves, enabling more aggressive updates and higher data efficiency.

This transition from the pre-power to power phase, marked by changes in the key constants, reflects the shift in Hessian values and parameter sensitivity. The LensLLM theory not only explains this complex behavior from first principles but also predicts when performance “qualitatively” improves with data input, guiding efficient data collection and model selection strategies.

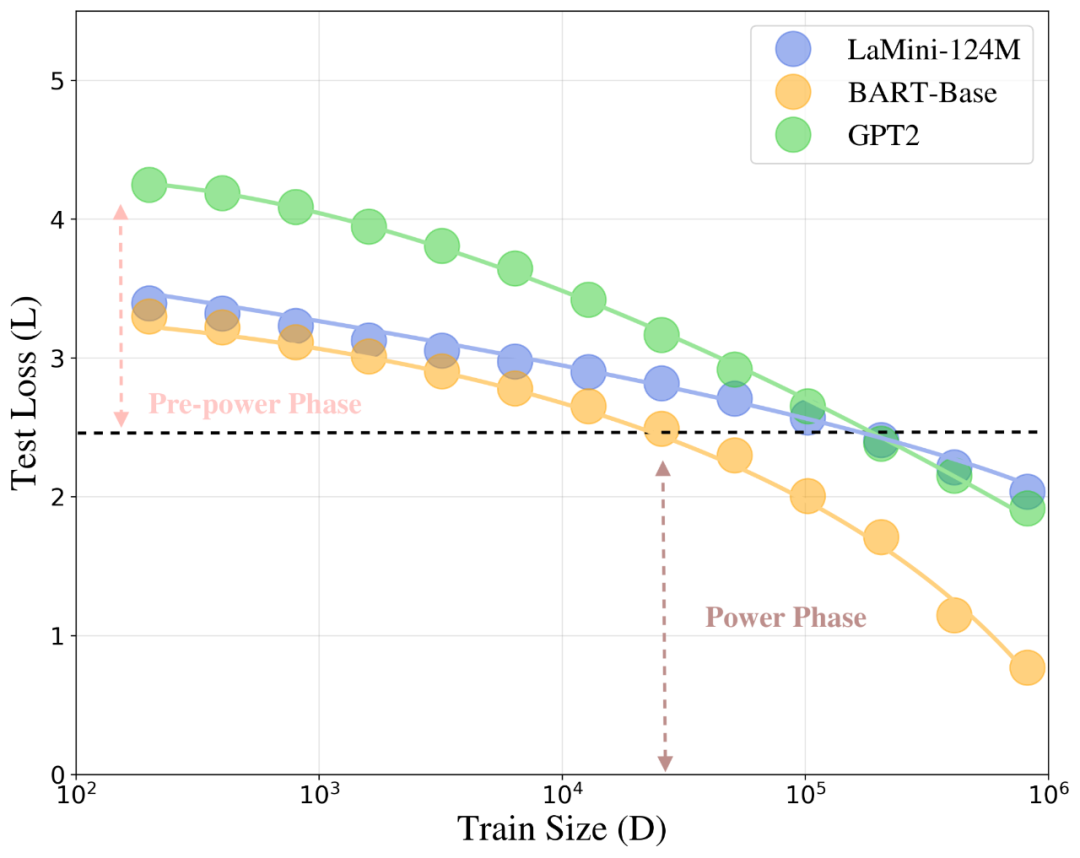
^{Figure 1: The phase transition phenomenon of test loss L during LLM fine-tuning as data size D varies. The low-data phase is pre-power, and the high-data phase is power, with a clear transition point.}

3. LensLLM: NTK-Driven “Transparent Eye” for Precise Performance Prediction

Building on the deep theoretical understanding of the phase transition mechanism, the team introduced LensLLM—a revolutionary NTK (Neural Tangent Kernel) enhanced correction scaling model. By incorporating NTK, LensLLM captures the complex dynamics of transformer architectures during fine-tuning, accurately representing how pretraining data influences performance. Its rigorous theoretical foundation provides a solid basis for model selection, moving beyond empirical fitting.

Key Advantage 1: Excellent curve fitting and prediction accuracy

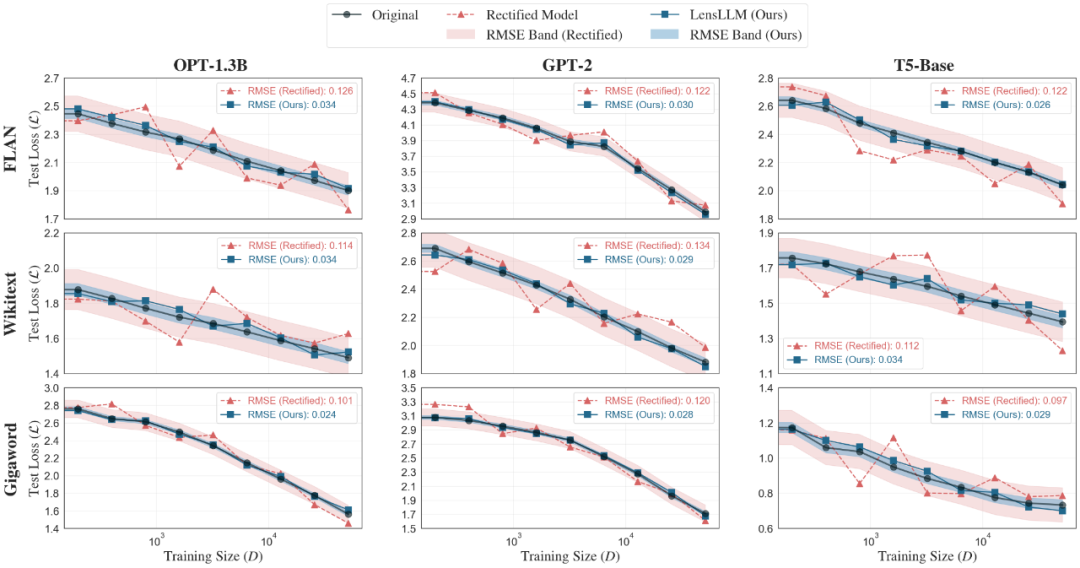
LensLLM demonstrates remarkable accuracy in curve fitting and test loss prediction. On benchmarks like FLAN, Wikitext, and Gigaword, LensLLM (blue squares) consistently outperforms baseline models (Rectified Scaling Law, red triangles), providing smoother, more accurate tracking of actual test loss curves with narrower RMSE bands.

In addition, the RMSE comparison shows that LensLLM’s prediction errors are significantly lower—often five times smaller—compared to the Rectified Scaling Law across datasets, confirming its superior stability and accuracy in modeling training dynamics.

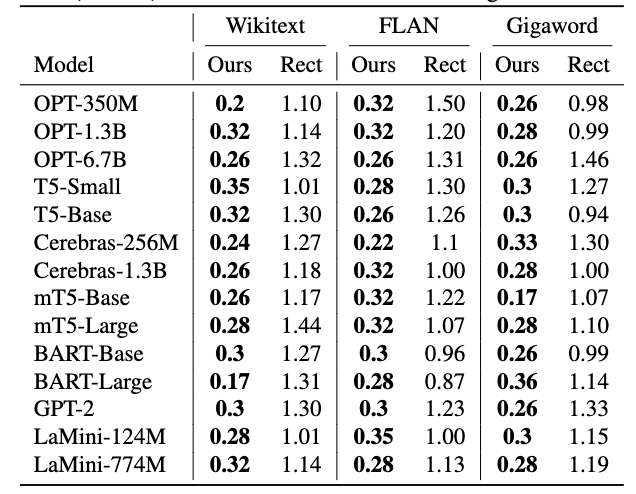
Figure 2: Performance curve fitting of LensLLM (blue squares) versus Rectified Scaling Law (red triangles) on datasets like FLAN, Wikitext, and Gigaword. LensLLM’s predictions are more accurate and stable, with lower RMSE.

Furthermore, the RMSE comparison shows that LensLLM’s errors are about one-fifth of the baseline, demonstrating its high precision in modeling training loss across multiple architectures and datasets.

Table 2: RMSE comparison of predicted versus actual test loss across datasets, showing LensLLM’s superior accuracy in modeling training dynamics.

In addition, LensLLM’s predictions of training loss are significantly more accurate, with errors about 5 times smaller than baseline models, across datasets like Wikitext, FLAN, and Gigaword, confirming its robustness and reliability.

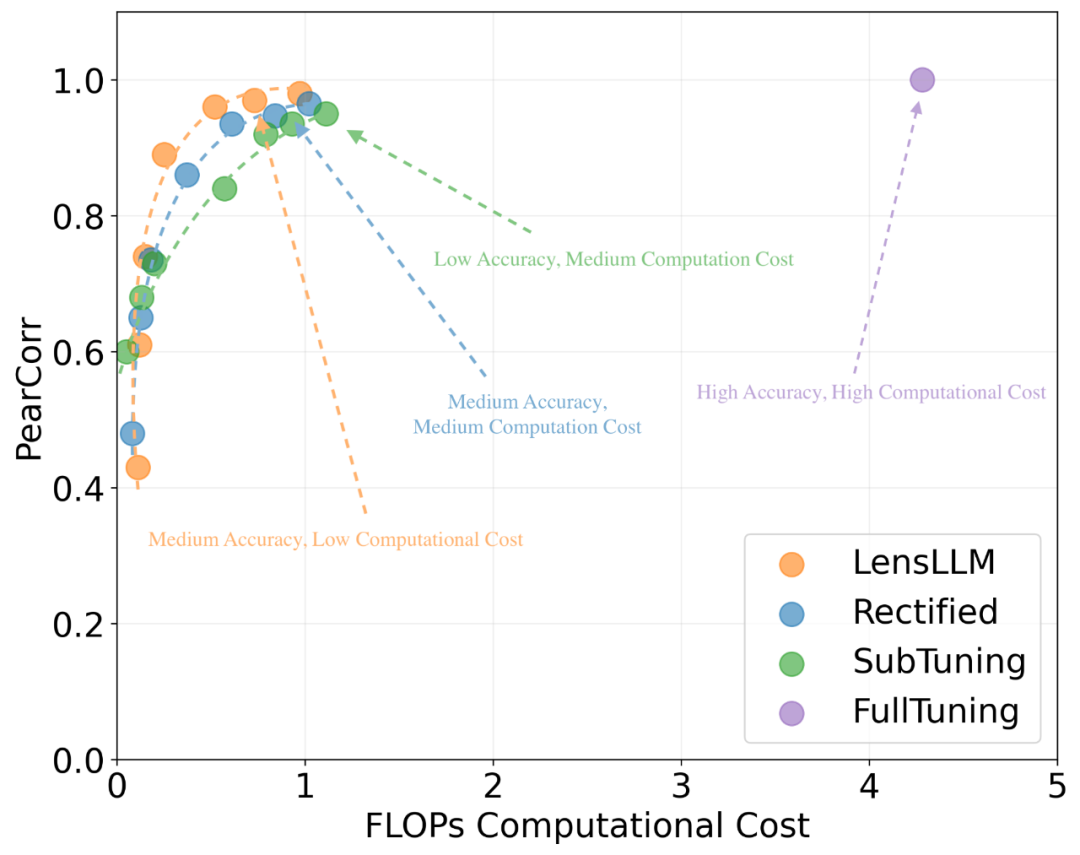
Figure 3: Performance of LensLLM (blue) versus baseline models in predicting Pearson correlation and relative accuracy across datasets. LensLLM consistently outperforms others, demonstrating excellent model selection capability.

More excitingly, LensLLM significantly reduces computational costs—up to 88.5% compared to full tuning! Its progressive sampling strategy allows high-performance model selection at much lower FLOPs, balancing efficiency and accuracy.

Figure 4: Pareto front of LLM model selection performance versus computational cost. LensLLM (orange point) achieves high Pearson correlation with significantly reduced FLOPs, outperforming baseline methods in efficiency.

4. Future Outlook: Expanding the Horizons of LLM Selection

This breakthrough provides researchers and engineers with powerful new tools to explore the potential of large models more confidently and efficiently. It not only sets a new benchmark for LLM selection but also opens up future possibilities, such as extending LensLLM to multi-task scenarios, exploring its impact on architecture design, and applying it to emerging models like MoE (Mixture of Experts).

Potential applications include:

• Model deployment in resource-constrained environments: LensLLM’s efficiency makes it ideal for edge devices and limited-resource scenarios, enabling rapid selection of performance-efficient models.
• A/B testing and iterative model development: Accelerates testing and deployment cycles, reducing trial-and-error costs.
• Personalized LLM customization: Quickly matching models to user data and tasks for optimal performance.

5. Conclusion

LensLLM acts as a beacon, illuminating the path toward efficient and precise model selection. It will end the “mysticism” of LLM fine-tuning and lead us into a new era of “intelligent” and “cost-effective” large model applications.