Flow Matching Becomes the Hot Topic at ICML 2025! Netizens: They Said Physicists Are Not Good at Switching to Computer Science}
Flow matching, integrating fluid dynamics into generative AI, is a trending topic at ICML 2025, with discussions highlighting the surprising influence of physics concepts in AI research.


As the 42nd International Conference on Machine Learning (ICML) approaches, taking place from July 13 to 19 in Vancouver, Canada, the latest frontier in generative AI has shifted towards higher quality, stability, simplicity, and universality of models.
Flow Matching technology is perfectly aligned with these hot topics.
Since the release of the FLUX model, flow matching architectures capable of handling various input types have become a focal point. Consequently, many scholars note that flow matching is almost ubiquitous in ICML 2025's generative work.

Although flow matching is at the forefront of AI research, its core concepts originate from fluid mechanics.
Surprisingly, ideas from physics have recently provided many new directions and breakthroughs in generative AI research, even extending to Schrödinger bridges in diffusion models.
On Zhihu, in the column "Deep Dive into Flow Matching", netizens have sharply commented: "Physicists should not be so quick to switch to computer science!"

- Column title: Deep Dive into Flow Matching
This article references the latest tweet by researcher Floor Eijkelboom, explaining the elegant and efficient generative technique by avoiding complex math formulas.
Generation: Noise to Data Mapping
Generation is a gradual process that starts from an abstract representation, passing through different networks, and finally producing detailed real data. The key challenge is mapping from a disordered noise distribution to complex data distributions, which is highly nonlinear and infinitely possible.

From a physics perspective, the core idea of flow matching is very simple: learn to convert noise into data.
It involves choosing an interpolation method (as shown in the figure) between the noise distribution and data distribution. Flow matching learns how to move each sample along this path, transforming initial noise points into data points at the end.

Flow matching is based on normalizing flows (NF), which use invertible transformations to map complex probability distributions to simple ones, enabling realistic data generation through inverse processes.
Flow Principle: Fluid Mechanics
Continuity Equation
How do we establish the interpolated path from noise to data? This question has been studied in fluid dynamics.
Tracking each tiny particle in a fluid is difficult; instead, physicists focus on the average density in a region, which is governed by the continuity equation.
This principle states that mass (or probability mass) is conserved—neither created nor destroyed—forming a direct link between physical concepts and probability distributions in generative models.

Continuity Equation: Also applies to probability mass
Intuitively, if inflow density exceeds outflow, density increases; if outflow exceeds inflow, density decreases; if balanced, density remains constant (equilibrium). The total outflow is called divergence.
Physicists derive overall density change laws from particle motion, but flow matching does the opposite: it specifies the density change process—interpolating from noise to data—and learns the velocity field that drives this evolution, enabling data generation from noise.
Process Illustration
Starting with a simple case—considering a single data point—
the process is defined by a straight path from noise to the data point, with velocity always pointing directly toward the target.
This is called conditional flow.

Flow matching's magic lies in how it handles the entire data distribution.
At any point in space, countless interpolation paths from noise to different data points pass through. The overall velocity field is the average direction of these paths at that point.

In high-probability regions, the paths tend to lead toward high-probability samples, and the average direction reflects this, guiding the generative process.
Training and Generation Illustration
In practice, the process involves sampling a data point x₁, a noise point x₀, and interpolating to an intermediate point x_t. The model learns the direction to move at this point.
Below is pseudocode illustrating this process:

Interested in flow matching? Check out the following paper:

- Paper title: Flow Matching for Generative Modeling
Diffusion and Flow Matching: Two Sides of the Same Coin
It’s clear that flow matching and diffusion models share similar forward processes.
What is their relationship?
MIT Associate Professor He Kai-ming believes that diffusion models are a subset of flow matching in the generative model domain.
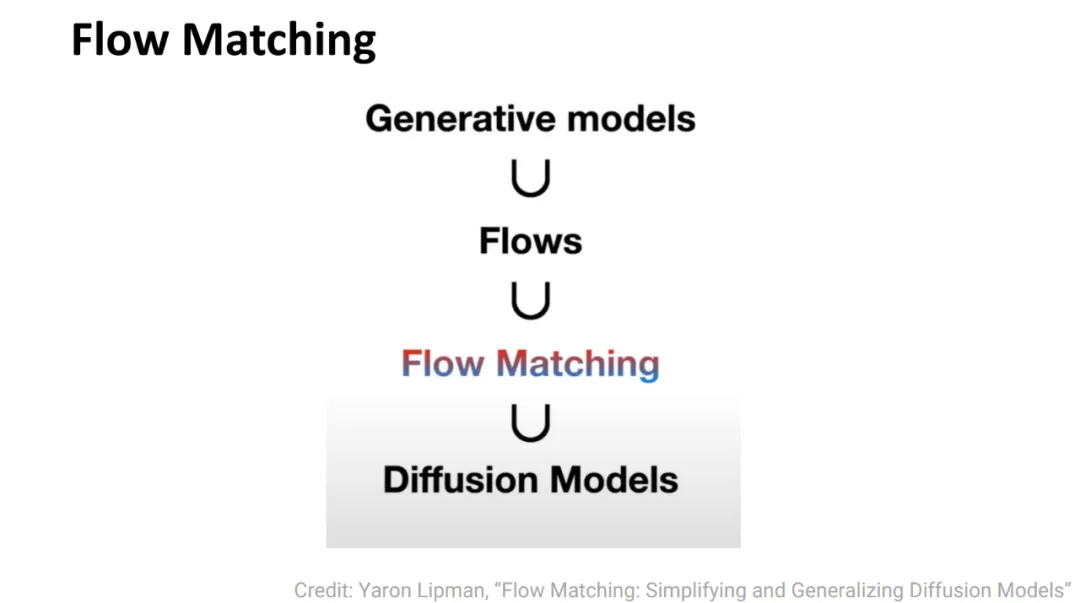
In fact, when using Gaussian distribution as the interpolation strategy, diffusion models are essentially a special case of flow matching.
This means the two frameworks can be used interchangeably.
Regarding the training process of diffusion models and flow matching:
- Consistency of weight functions: The weight functions used during training are crucial, balancing the importance of different frequency components in perceptual data. Flow matching's weight design aligns closely with that in diffusion literature.
- Noise scheduling has minimal impact on training objectives: While it affects training efficiency, it does not significantly influence the ultimate training goal.
- Differences in network output forms: Flow matching introduces a new parameterization of network outputs as a velocity field, differing from traditional diffusion models' outputs. This may affect performance with higher-order samplers and training dynamics.
More information on the relationship between diffusion models and flow matching can be found in the following articles:

- Article title: Diffusion Meets Flow Matching: Two Sides of the Same Coin
References: