Farewell to Data 'Noise': UCSD's New Reasoning Method DreamPRM Acts as a 'Signal Amplifier' Tops MathVista Rankings}

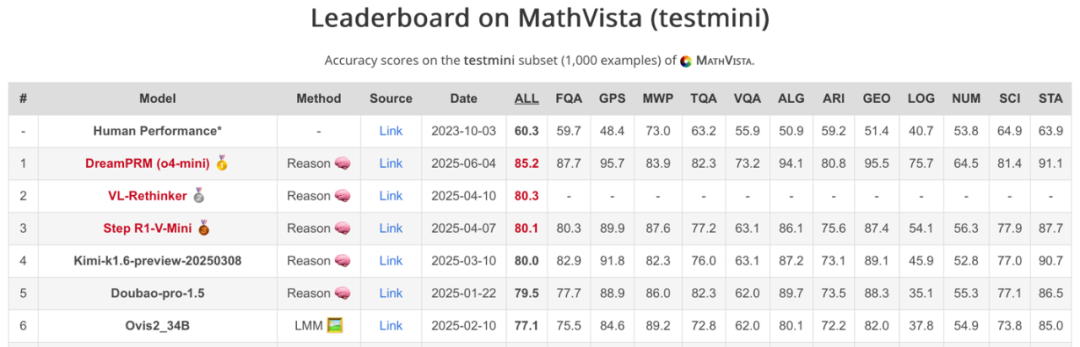
DreamPRM, developed by a research team at UC San Diego, achieved first place on the authoritative MathVista reasoning leaderboard. The first author is PhD student Qi Cao, with associate professor Pengtao Xie as the corresponding author. Other team members include Ruiyi Wang, Ruiyi Zhang, and Sai Ashish Somayajula.

Using reinforcement learning with process rewards (PRM) to enhance reasoning in pure text tasks has shown significant success. However, extending this to multimodal large language models (MLLMs) faces two major challenges:

• High-dimensional, mixed signals from multimodal inputs (images + text) cause distribution shifts that reduce generalization ability.
• Data imbalance: many low-value samples in open-source multimodal datasets dilute supervision signals for key reasoning steps like cross-modal logic linking.

To address these issues, a dual-level optimization framework was proposed, treating domain weights as learnable parameters to dynamically suppress low-quality data and emphasize high-information-density data, balancing coverage and quality.

• Paper Title: DreamPRM: Domain-Reweighted Process Reward Model for Multimodal Reasoning
• Code Repository: https://github.com/coder-qicao/DreamPRM

DreamPRM's core innovation is a differentiable dual-level optimization process that dynamically adjusts domain weights to mitigate distribution shifts and data imbalance in multimodal reasoning.

In the lower optimization stage, the model trains PRM parameters across 15 diverse domains, each assigned a dynamic weight reflecting its contribution to the overall loss. Monte Carlo supervision estimates the quality of intermediate reasoning steps, guiding parameter updates via a weighted MSE loss.

In the upper stage, the system uses a curated meta-dataset covering 30 disciplines and 183 subfields to evaluate generalization. It minimizes the discrepancy between aggregated process evaluation and final answer accuracy, updating domain weights through backpropagation.

This creates a positive feedback loop: high-quality data domains (e.g., those requiring complex cross-modal reasoning like M3CoT) gain higher weights, while simpler domains (e.g., AI2D) are down-weighted. The process converges to a distribution aligned with data quality and density.

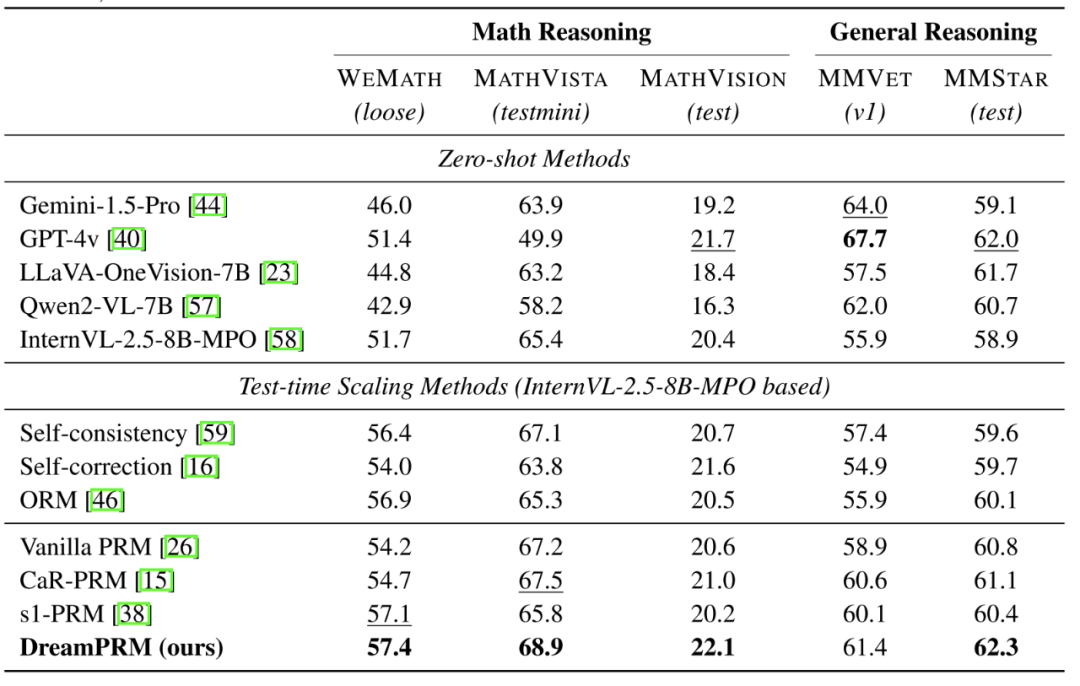
Experimental Results

Key Performance Highlights

• Significant domain re-weighting advantage: DreamPRM outperforms other PRM methods across five benchmarks, with 2-3% improvements over unweighted PRM. Its automatic domain weight strategy surpasses heuristic rules, demonstrating data-driven effectiveness.
• Small models outperform large ones: DreamPRM enables an 8B parameter model (InternVL-2.5-8B-MPO) to outperform larger closed-source models like GPT-4v and Gemini-1.5 on most benchmarks, showcasing strong reasoning capabilities.
• Fine-grained evaluation boosts performance: Process supervision with step-by-step scoring exceeds other test-time optimization methods, confirming the importance of detailed evaluation.

Scaling Experiments

• Performance improves steadily with more candidate reasoning chains (CoT). When increasing from 2 to 8 chains, accuracy on all five benchmarks continues to rise.
• Seamless transfer to stronger multimodal models: Applying DreamPRM to GPT-4.1-mini and o4-mini improves accuracy on MathVista benchmarks, demonstrating excellent generalization.

Learned Domain Weights

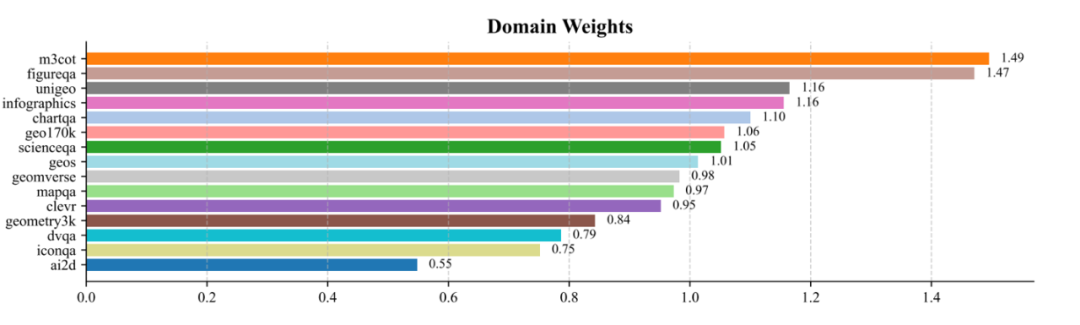
Final domain weights range from 0.55 to 1.49, with datasets like M3CoT and FigureQA receiving the highest weights (~1.5), while datasets like AI2D and IconQA have lower weights (<0.8). This distribution confirms the significant quality differences across datasets and enhances PRM performance.

Summary

DreamPRM's innovative dual-level optimization effectively addresses data imbalance and distribution shift in multimodal reasoning, leading to consistent improvements across benchmarks, especially in complex math reasoning tasks.