At 47, He Switched Fields and Unlocked the Largest Unsolved Problem in Sphere Packing}

In mathematics, the quest for optimal packing patterns is endless, and the sphere packing problem is no exception. It aims to efficiently pack spheres into a (high-dimensional) box, with significant applications in cryptography, communications, and more.

It appears simple but is subtly complex. In the early 17th century, astronomer and mathematician Johannes Kepler proved that packing spheres in three dimensions like stacking oranges fills about 74% of space. He hypothesized this was the optimal arrangement, but it took nearly 400 years for mathematicians to prove this.

In higher dimensions, the exact solutions remain unknown, except for the 8- and 24-dimensional cases. Over the years, incremental improvements have been made, but these are small and rare.

Recently, Boaz Klartag, a mathematician, published a paper in April titled "Lattice packing of spheres in high dimensions using a stochastically evolving ellipsoid," which broke previous records with a significant advantage. Some researchers even believe his results may be close to optimal.

Paper link: https://arxiv.org/pdf/2504.05042

As a newcomer to this field, Klartag revived an ancient technique abandoned decades ago by experts, applying it to all high-dimensional spaces. His work touches on long-standing debates about the nature of optimal sphere packings—should they be ordered or disordered? How densely can spheres be packed?

“This is truly a remarkable breakthrough,” said Gil Kalai, a mathematician at the Hebrew University of Jerusalem. “It’s a result that has excited mathematicians for nearly a century.”

Two directions in the field

In 1905, German mathematician Hermann Minkowski developed an intuitive approach to sphere packing, starting with a lattice—repeating points in space—and placing spheres around each point. The problem of finding the densest packing then reduces to finding the most efficient lattice arrangement. In 2D, the optimal lattice is hexagonal, as shown below:

Seems intuitive? But in 1947, mathematician Claude Ambrose Rogers proposed a different view. He argued that one could start from any lattice—even suboptimal ones—and instead of spheres, place ellipsoids (elliptical shapes) that touch but do not extend beyond neighboring points. Rogers developed an algorithm to build dense sphere packings based on these ellipsoids.

How does it work?

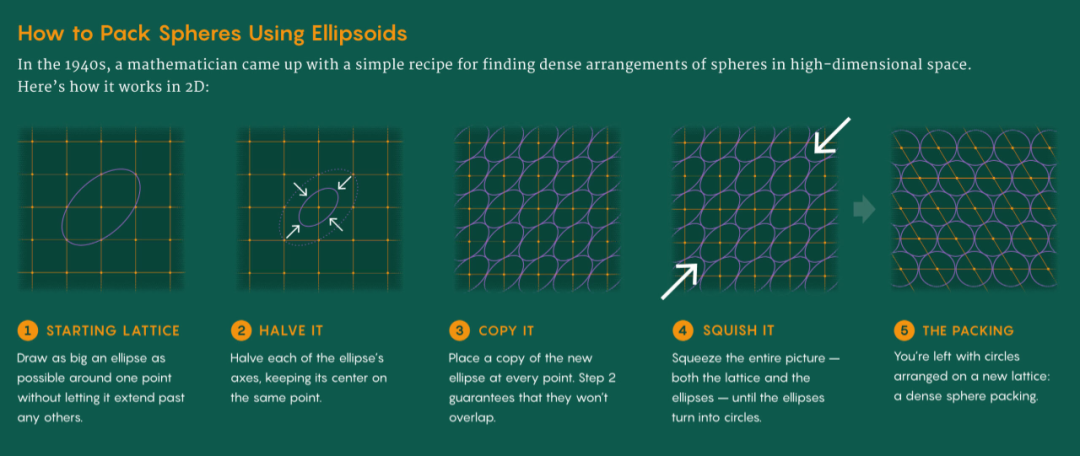
Rogers’ method’s advantage is that you don’t need to start with an optimal lattice; choosing the right ellipsoid shape is key. Unlike spheres defined by a single radius, ellipsoids are defined by multiple axes, increasing complexity in higher dimensions.

“In high-dimensional space, it’s unclear how to extend these shapes—there are too many degrees of freedom,” Klartag said.

Ultimately, mathematicians returned to Minkowski’s lattice approach, focusing on finding suitable lattices rather than geometric shapes. This led to incremental improvements, but significant breakthroughs remained elusive for decades. Only an outsider like Klartag could break this stagnation.

External perspective

Klartag, a mathematician at the Weizmann Institute of Science in Israel, has long been interested in lattices and sphere packing. However, he lacked time for deep research, as his main focus was on convex geometry, which involves shapes with various symmetries, especially in high dimensions. Klartag believed these tools were underestimated in their power.

“Boaz Klartag has long thought that methods from convex geometry could help solve sphere packing problems. He just never had the time to verify his hypothesis—until now,”

Last November, after completing an important project in his usual research area, he found his schedule unexpectedly cleared. “I’m 47 now, and I’ve always wanted to study lattices. If I don’t do it now, I never will,” he said. He sought guidance from his friend Barak Weiss at Tel Aviv University.

Klartag and Weiss, along with a few others, held a small seminar to review relevant literature. Klartag carefully studied Minkowski’s and Rogers’ methods.

When he read about Rogers’ technique of transforming ellipsoids into sphere packings, he wondered why mathematicians had abandoned this approach. Since ellipsoids are convex, Klartag knew many complex methods to manipulate them. He realized that Rogers’ initial ellipsoid was intuitive but inefficient. He could construct a better ellipsoid—one that covers more space before touching the boundary of the lattice points—and thus create new packing records.

He first used a familiar method: expanding and contracting the ellipsoid along each axis via a random process. When the boundary reached enough to touch a new lattice point, he froze growth in that direction. This ensured the point would never fall inside the ellipsoid. The shape continued to expand in other directions until it hit another point. The ellipsoid thus changed shape rapidly and hesitantly, exploring the surrounding space. Over time, the boundary would encounter enough points to stop further growth.

As time passed, the volume of the ellipsoid generally increased. But would it grow enough to surpass Rogers’ original ellipsoid?

Since Klartag’s method is random, each implementation produces a different ellipsoid. He evaluated the possible volume range of these ellipsoids. If he could find one larger than Rogers’ ellipsoid, he could convert it into a denser sphere packing using Rogers’ original method.

He couldn’t find a sufficiently large ellipsoid, so he refined the growth process. Within a few weeks, he proved that, at least at times, the process could produce a sufficiently large ellipsoid to set a new record.

He immediately shared the results with Weiss. “Let’s meet next week. I’ll tell you how I was wrong,” Klartag said confidently, feeling more assured about his proof.

Close to the truth

The new proof was verified. Klartag’s initial ellipsoid, transformed into a sphere packing, achieved the most significant efficiency improvement since Rogers’ 1947 paper. For a given dimension d, Klartag’s packing could fit roughly d times more spheres than previous results. In 100 dimensions, he could pack about 100 times more spheres; in a million dimensions, about a million times more.

In just a few months of research and weeks of proof, Klartag cracked a core problem in lattice and sphere packing. “It feels almost unfair,” he said. But mathematics often works this way: sometimes, a tough problem only needs a new idea, and exploring outside one’s field can pay off. His familiarity with convex geometry, usually a different area, was exactly what the problem needed. “My work kept this idea in my mind,” he said. “It was clearly worth trying.”

His achievement reignited debates about the optimality of high-dimensional packings. For a long time, mathematicians believed that highly symmetric, lattice-based packings were the densest. But in 2023, a team discovered a non-lattice packing that surpassed previous records. Klartag’s work supports the view that disorder might be key to optimality.

Furthermore, the question of how dense sphere packings can be remains controversial. Some believe Klartag’s method is nearly optimal—already close to the maximum—while others see room for improvement. “I really don’t know what to believe now,” said Marcus Michelen of the University of Chicago. “All options seem open.”

This problem is crucial for applications in cryptography and communications. Although Klartag’s results don’t have immediate practical effects, they have sparked initial enthusiasm. “This problem is very challenging for engineers and has seen little progress in recent years,” said Or Ordentlich, an information theorist at the Hebrew University. “So, we’re excited.”

Klartag hopes his work will revive the practical use of lattice and convex geometry, linking these fields more closely than before. “I believe our understanding of convex bodies should benefit lattice theory, even surpassing packing theory,” he said. “My goal is to strengthen the connection between these areas. That’s my plan, and I want to keep going.”

^Reference:

^{https://www.quantamagazine.org/new-sphere-packing-record-stems-from-an-unexpected-source-20250707/}